Trọng tâm là gì? Công thức tính trọng tâm của tam giác

Trọng tâm của tam giác là 1 trong trong mỗi kỹ năng và kiến thức rất rất cần thiết và thịnh hành trong mỗi năm học tập phổ thông. Bài viết lách sau đây, Quantrimang.com xin xỏ reviews với chúng ta những kỹ năng và kiến thức tương quan cho tới trọng tâm tam giác, công thức tính trọng tâm tam giác, công thức tính tọa chừng trọng tam giác, mời mọc chúng ta xem thêm nhằm phần mềm nhập giải những Việc nhập quy trình học hành nhé.

Trọng tâm là gì?

Ba lối trung tuyến của một tam giác nằm trong trải qua một điểm.
Điểm bắt gặp nhau của tía lối trung tuyến gọi là trọng tâm của tam giác.

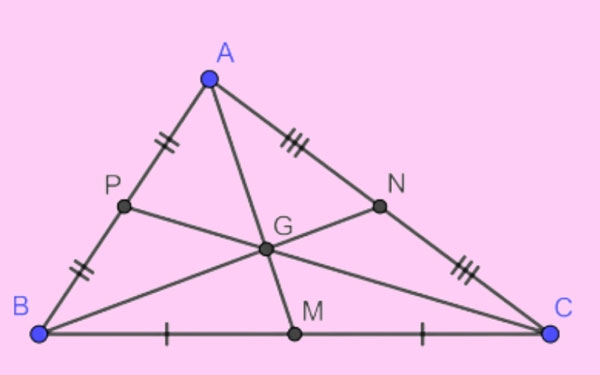
Tính hóa học của trọng tâm nhập tam giác

Khoảng cơ hội kể từ trọng tâm của tam giác cho tới đỉnh vày 2/3 chừng nhiều năm lối trung tuyến ứng với đỉnh cơ.

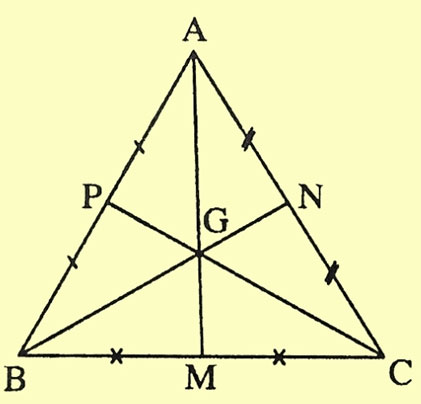
Tam giác ABC, với những lối trung tuyến AM, BN, CP và trọng tâm G, tao có:

Tính hóa học trọng tâm của tam giác

Trọng tâm tam giác vuông

Trọng tâm của tam giác vuông cũng khá được xác lập tựa như trọng tâm của tam giác thông thường.

Tam giác MNP vuông bên trên M.

3 lối trung tuyến MD, NE, PF phó nhau bên trên trọng tâm O. Ta với MD là trung tuyến của góc vuông PMN nên MD = 50% PN = DP = Doanh Nghiệp.

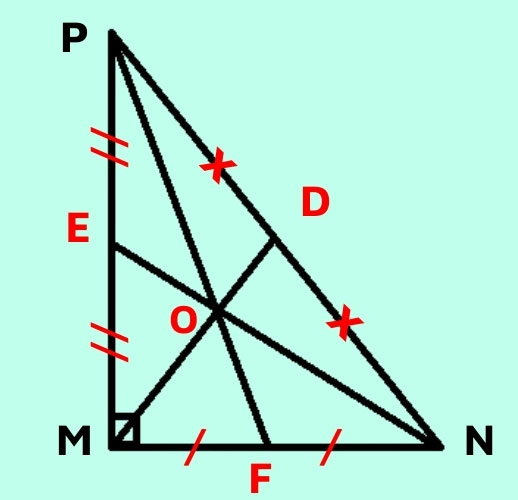
Trọng tâm tam giác vuông

Trọng tâm tam giác cân

Tam giác ABC cân nặng bên trên A, với G là trọng tâm.

Vì tam giác ABC cân nặng bên trên A nên AG vừa phải là lối trung tuyến, lối cao, lối trung trực và là lối phân giác, kể từ cơ tao suy rời khỏi được hệ trái khoáy của trọng tâm tam giác cân nặng ABC như sau:

Góc BAD vày góc CAD.
Trung tuyến AD vuông góc với cạnh lòng BC.

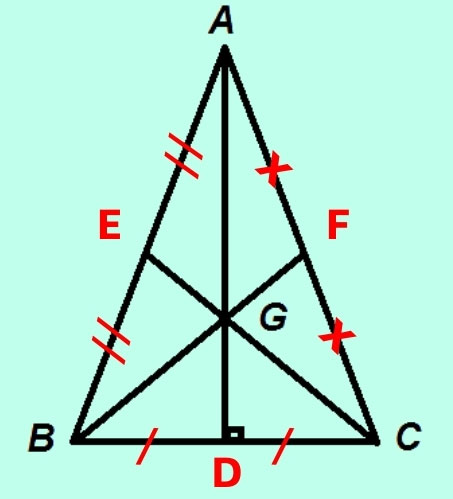
Trọng tâm tam giác cân

Trọng tâm của tam giác vuông cân

Có tam giác ABC vuông cân nặng bên trên A và I là trọng tâm. AM là lối trung trực, lối trung tuyến, lối phân giác và lối cao của tam giác này nên AM vuông góc với BC.

Mặt không giống, vì như thế tam giác ABC vuông cân nặng bên trên A nên:

AB = AC.

=> BP = công nhân và BN = AN = CP = AP.

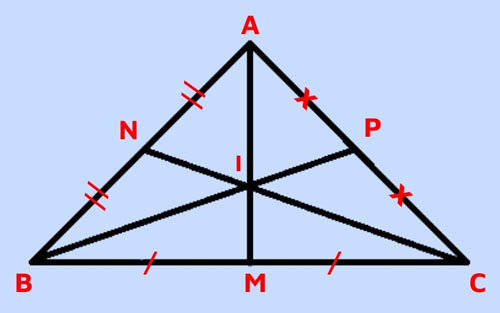
Trọng tâm tam giác vuông cân

Trọng tâm tam giác đều

Tam giác ABC đều, G là phó điểm tía lối trung tuyến, lối cao, lối phân giác.

Vì vậy bám theo đặc điểm của tam giác đều tao với G vừa phải là trọng tâm, trực tâm, tâm lối tròn xoe nước ngoài tiếp và nội tiếp của tam giác ABC.

Trọng tâm tam giác đều

Cách tìm hiểu trọng tâm tam giác

Cách 1: Giao điểm 3 lối trung tuyến

Xác tấp tểnh trọng tâm tam giác bằng phương pháp lấy phó điểm của tía lối trung tuyến.

Bước 1: Vẽ tam giác ABC, theo thứ tự xác lập trung điểm của những cạnh AB, BC, CA.

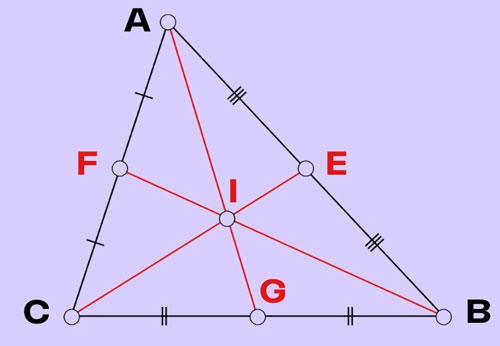
Bước 2: Nối theo thứ tự những đỉnh cho tới trung điểm của cạnh đối lập. Nối A với G, B với F, C với E.

Bước 3: Giao điểm I của tía lối trung tuyến là AG, BF, CE là trọng tâm của tam giác ABC.

Giao điểm 3 lối trung tuyến

Cách 2: Tỉ lệ bên trên lối trung tuyến

Xác tấp tểnh trọng tâm tam giác dựa vào tỉ trọng lối trung tuyến.

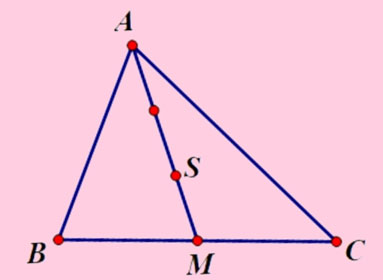
Bước 1: Vẽ tam giác ABC, xác lập trung điểm M của cạnh BC.

Bước 2: Nối đỉnh A với trung điểm M, tiếp sau đó lấy điểm S sao cho tới AS = 2/3 AM.

Theo đặc điểm trọng tâm tam giác thì điểm S đó là trọng tâm tam giác ABC.

Xác tấp tểnh trọng tâm tam giác dựa vào tỉ trọng lối trung tuyến.

Bài tập luyện về trọng tâm tam giác

Dạng 1: Sử dụng đặc điểm trọng tâm tam giác

Phương pháp giải

- Ba lối trung tuyến của tam giác đồng quy bên trên một điểm. Điểm này gọi là trọng tâm của tam giác.

- Trọng tâm của tam giác cơ hội từng đỉnh một khoảng chừng vày 2/3 chừng nhiều năm lối trung tuyến trải qua đỉnh ấy.

Bước 1. Xác tấp tểnh trọng tâm phía trên lối trung tuyến nào là.

Bước 2. Sử dụng linh động tỉ trọng khoảng cách kể từ trọng tâm cho tới nhì đầu đoạn trực tiếp trung tuyến.

Ví dụ 1: Cho tam giác ABC với hai tuyến phố trung tuyến BM, công nhân rời nhau bên trên G. Chứng minh rằng: $BM + công nhân > \frac{3}{2}BC$ .

Hướng dẫn giải

Hình vẽ minh họa:

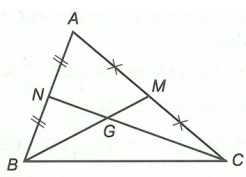
Trọng tâm là gì? Công thức tính trọng tâm của tam giác

Xét tam giác ABC với hai tuyến phố trung tuyến BM và công nhân rời nhau bên trên G.

Suy rời khỏi G là trọng tâm tam giác ABC

$\Rightarrow BG = \frac{2}{3}BM;CG = \frac{2}{3}CN$

Do cơ tao nên minh chứng $\frac{3}{2}BG + \frac{3}{2}CG > \frac{3}{2}BC$ hoặc $BG + CG > BC\left( 1 \right)$

Bất đẳng thức (1) luôn luôn đích vì như thế nhập một tam giác tổng chừng nhiều năm nhì cạnh to hơn chừng nhiều năm cạnh còn sót lại.

Vậy $BM + công nhân > \frac{3}{2}BC$ , (điều nên hội chứng minh).

Ví dụ 2. Cho tam giác ABC. Trên cạnh BC lấy điểm G sao cho tới BG = 2GC. Vẽ điểm D sao cho tới C là trung điểm của AD. Gọi E là trung điểm của BD.

Chứng minh:

a) Ba điểm A, G, E trực tiếp sản phẩm.

b) Đường trực tiếp DG trải qua trung điểm của AB.

Hướng dẫn giải

Hình vẽ minh họa

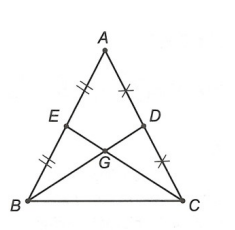
Trọng tâm là gì? Công thức tính trọng tâm của tam giác

a) Xét tam giác ABD với C là trung điểm của cạnh AD

=> BC là trung tuyến của tam giác ABD.

Hơn nữa G ∈ BC và GB = 2GC

=> $GB = \frac{2}{3}BC$

=> G là trọng tâm tam giác ABD.

Lại với AE là lối trung tuyến của tam giác ABD nên A, G, E trực tiếp sản phẩm.

b) Ta với G là trọng tâm tam giác ABD

=> DG là lối trung tuyến của tam giác này.

Suy rời khỏi DG trải qua trung điểm của cạnh AB (điều nên hội chứng minh).

Dạng 2: Chứng minh một điểm là trọng tâm tam giác

Phương pháp giải

Sử dụng đặc điểm trọng tâm. Chẳng hạn nhằm minh chứng G là trọng tâm tam giác ABC, với tía lối trung tuyến AD, BE, CF thì tao hội chứng minh:

Cách 1.

$G \in AD;GA = \frac{2}{3}AD$

Hoặc $G \in BE;GB = \frac{2}{3}BE$

Hoặc $G \in CF;GC = \frac{2}{3}CF$

Cách 2.

Chứng minh G là phó điểm của nhì nhập tía lối trung tuyến của tam giác ABC.

Ví dụ 1: Cho tam giác ABC với lối trung tuyến AD, bên trên đoạn trực tiếp AD lấy nhì điểm E, G sao cho tới AE = EG = GD. Chứng minh G là trọng tâm tam giác ABC.

Hướng dẫn giải

Hình vẽ minh họa

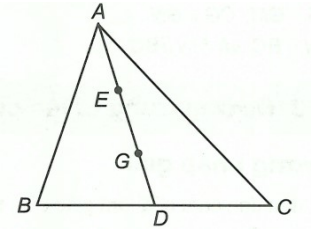
Trọng tâm là gì? Công thức tính trọng tâm của tam giác

Ta với AD = AE + EG + GD nhưng mà AE = EG = GD nên AD = 3AE

$\Rightarrow AE = EG = GD = \frac{1}{2}AD \Rightarrow AG = \frac{2}{3}AD$

Vì AD là lối trung tuyến và $AG = \frac{2}{3}AD$ nên G là trọng tâm tam giác ABC.

Ví dụ 2: Cho tam giác ABC, D là trung điểm của AC. Trên đoạn BD lấy điểm E sao cho tới BE = 2ED. Điểm F nằm trong tia đối của tia DE sao cho tới BF = 2BE. Gọi K là trung điểm của CF và G là phó điểm của EK với AC.

a) Chứng minh G là trọng tâm tam giác EFC.

b) Tính những tỉ số $\frac{{GE}}{{GK}};\frac{{GC}}{{DC}}$

Hướng dẫn giải

Hình vẽ minh họa

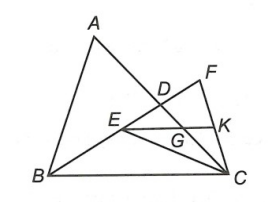
Trọng tâm là gì? Công thức tính trọng tâm của tam giác

a) Ta với BF = 2BE; BE = EF

Mà BE = 2ED nên EF = 2ED

=> D là trung điểm của EF

=> CD là lối trung tuyến của tam giác EFC.

Vì K là trung điểm của CF nên EK là lối trung tuyến của tam giác EFC.

Tam giác EFC với hai tuyến phố trung tuyến CD và EK rời nhau bên trên G nên G là trọng tâm của tam giác EFC.

b) Ta với G là trọng tâm tam giác EFC nên $\frac{{GC}}{{DC}} = \frac{2}{3};GE = \frac{2}{3}EK$

$\Rightarrow GK = \frac{1}{3}EK \Rightarrow GE = 2GK \Rightarrow \frac{{GE}}{{GK}} = 2$

Dạng 3. Đường trung tuyến của tam giác cân nặng, tam giác đều, tam giác vuông

Phương pháp giải

Chú ý cho tới đặc điểm của tam giác cân nặng, tam giác đều và tam giác vuông.

Ví dụ: Cho tam giác đều ABC với tía lối trung tuyến AD, BE, CF rời nhau bên trên G.

Chứng minh:

a) AD = BE = CF.

b) GA = GB = GC.

Hướng dẫn giải

Hình vẽ minh họa

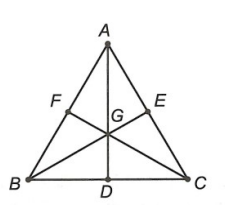
Trọng tâm là gì? Công thức tính trọng tâm của tam giác

a) Ta với BE; CF là những lối trung tuyến của tam giác ABC

=> $CE = \frac{1}{2}AC;BF = \frac{1}{2}AB$

Vì AC = AB nên $\frac{1}{2}AC = \frac{1}{2}AB$ hoặc CE = BF.

Xét tam giác BCE và tam giác CBF có

BC chung; $\widehat {BCE} = \widehat {CBF}$ (do tam giác ABC cân nặng ở A); CE = BF (chứng minh trên).

Do cơ ∆BCE = ∆CBF (c.g.c)

=> BE = CF (2 cạnh tương ứng).

Chứng minh tương tự động tao với AD = BE.

Từ cơ suy rời khỏi AD = BE = CF (điều nên hội chứng minh).

b) Vì G là trọng tâm tam giác ABC nên $AG = \frac{2}{3}AD;BG = \frac{2}{3}BE;CG = \frac{2}{3}CF$

Vì AD = BE = CF (theo minh chứng câu a) nên $\frac{2}{3}AD = \frac{2}{3}BE = \frac{2}{3}CF$ hoặc GA = GB = GC (điều nên hội chứng minh)

Bài 1:

Tam giác ABC với trung tuyến AD = 9cm và trọng tâm I. Tính chừng nhiều năm đoạn AI?

Giải:

Ta với I là trọng tâm của tam giác ABC và AD là lối trung tuyến nên AI = (2/3) AD (theo đặc điểm tía lối trung tuyến của tam giác).

Do đó: AG = (2/3).9 = 6 (cm).

Vậy đoạn AI có tính nhiều năm 6 centimet.

Tam giác ABC với trung tuyến AD = 9cm và trọng tâm I

Bài 2:

Cho I là trọng tâm của tam giác đều MNP. Chứng minh rằng: IM = IN = IP.

Giải:

Gọi trung điểm MN, MP, PN theo thứ tự là R, O, S.

Khi cơ MS, quảng bá, NO đồng quy bên trên trọng tâm I.

Ta với ∆MNP đều, suy ra:

MS = quảng bá = NO (1).

Vì I là trọng tâm của ∆ABC nên bám theo đặc điểm lối trung tuyến:

MI = 2/3 MS, PI = 2/3 quảng bá, NI = 2/3 NO (2).

Từ (1) , (2) ⇒ GA = GB = GC.

Tọa chừng của trọng tâm tam giác nhập mặt mày phẳng lặng Oxy

Cho tam giác ABC với A(xA; yA), B(xB; yB), C(xC; yC). Nếu G là trọng tâm của tam giác ABC thì:

$\left\{\begin{array}{l}x_G=\frac{x_A+x_B+x_C}{3} \\ y_G=\frac{y_A+y_B+y_C}{3}\end{array}\right.$

Ví dụ 1: Trong mặt mày phẳng lặng tọa chừng Oxy, cho những điểm A(2; 0), B(0; 4), C(1; 3).

a, Chứng minh rằng A, B, C là 3 đỉnh của một tam giác.

b, Tìm tọa chừng nhập tâm tam giác ABC.

Hướng dẫn giải:

a, Ta có: =(-2; 4) và =(-1; 3)

Do $\frac{-2}{-1}\ne\frac{4}{3}$ nên $\overrightarrow{AB},\overrightarrow{\ AC}$ không nằm trong phương, suy rời khỏi A, B, C ko trực tiếp sản phẩm.

Vậy A, B, C là 3 đỉnh của một tam giác.

b, Gọi G là trọng tâm tam giác ABC. Suy rời khỏi tọa chừng của G là:

$\left\{\begin{array}{l} x_G=\frac{x_A+x_B+x_C}{3}=\frac{2+0+1}{3}=1 \\ y_G=\frac{y_A+y_B+y_C}{3}=\frac{0+4+3}{3}=\frac{7}{3} \end{array}\right.$

Vậy tọa chừng trọng tâm tam giác ABC là G (1; $\frac{7}{3}$ ).

Ngoài định nghĩa và những công thức về trọng tâm tam giác phía trên, những chúng ta cũng có thể tìm hiểu hiểu thêm thắt những kỹ năng và kiến thức không giống về tam giác như diện tích S tam giác, chu vi tam giác, lối cao tam giác.