Trong môn đại số và hình học tập giải tích, ma trận chuyển cơ sở là một trong định nghĩa cần thiết . Nó được dùng nhằm tế bào mô tả một luật lệ chuyển đổi tuyến tính thân ái nhị không khí vector đem nằm trong số chiều cùng nhau. Sau phía trên, hãy nằm trong lần hiểu khái niệm và bài bác luyện và cơ hội lần ma trận chuyển cơ sở nhé!!!
Xem thêm:
- định thức quái trận
- hạng của quái trận
- bài luyện quái trận đem tiếng giải
I. Định nghĩa ma trận chuyển cơ sở
Ma trận gửi hạ tầng là quái trận quy đổi tọa phỏng của một vectơ kể từ hạ tầng này thanh lịch hạ tầng không giống.. Ma trận gửi S→T là quái trận toạ phỏng của T bám theo S.
Muốn lần ma trận chuyển cơ sở kể từ S thanh lịch T, kí hiệu P(S→T), tao cần thiết lần tọa phỏng của những vector vô hạ tầng T so với hạ tầng S, tiếp sau đó ghi chép quái trận bám theo quy tắc, từng tọa phỏng là một trong cột của quái trận bám theo trật tự.
Ngược lại, mong muốn lần ma trận chuyển cơ sở kể từ T thanh lịch S, kí hiệu P(T→S), tao cần thiết lần tọa phỏng của những vector vô S so với hạ tầng T và ghi chép quái trận bám theo quy tắc bên trên.
Ví dụ: Trong không khí \(R^{3}\) cho 2 hệ cơ sở:
\(S={u_{1}(1,1,1) , u_{2}(1,0,2), u_{3}(1,2,1)}\) \(T={v_{1}(2,3,2) , v_{2}(-1,1,4), v_{3}(2,1,3)}\)
Tìm ma trận chuyển cơ sở kể từ S thanh lịch T.
Giải
Xét quái trận sau:
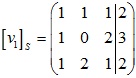
Giải hệ phương trình:
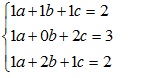
ta được 3 nghiệm a=1,b=0,c=1.
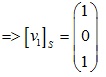
Tương tự động xét quái trận:
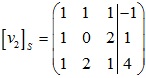
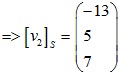
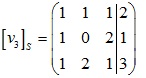
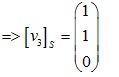
Vậy quái trận cần thiết lần là:
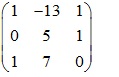
Xem thêm:
- hệ phương trình tuyến tính – Bài luyện đem tiếng giải PP Gauss
- chéo hoá quái trận
- ánh xạ tuyến tính
III. Bài luyện ma trận chuyển cơ sở
1. Tìm ma trận chuyển cơ sở kể từ u thanh lịch v
Bài toán: Xét không khí \(R^{3}\) với 2 cơ sở:
\(u_{1}(1,0,0); u_{2}(0,1,0); u_{3}(0,0,1) và v_{1}(1,1,0); v_{2}(0,1,1); v_{3}(1,0,1)\)
a) Tìm quái trận gửi kể từ hạ tầng (u) thanh lịch hạ tầng (v)
b) Tìm quái trận gửi kể từ hạ tầng (v) thanh lịch hạ tầng (u)
Hướng dẫn giải

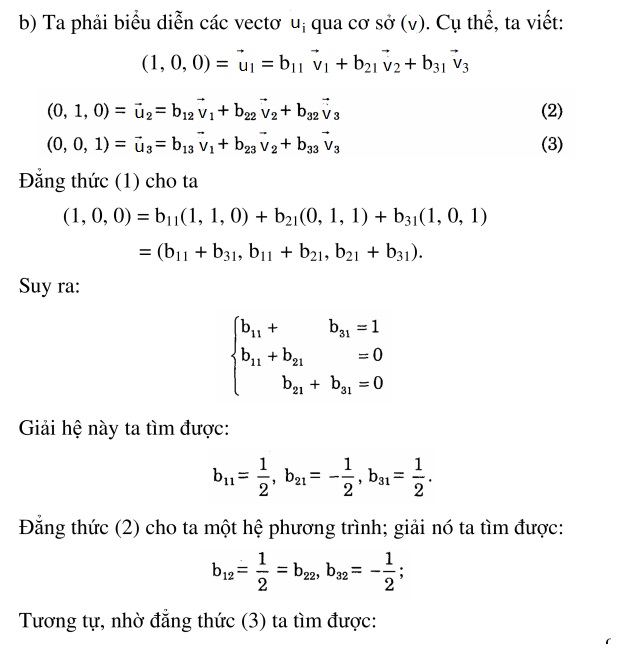

2. Ma trận gửi kể từ hạ tầng u thanh lịch hạ tầng v là


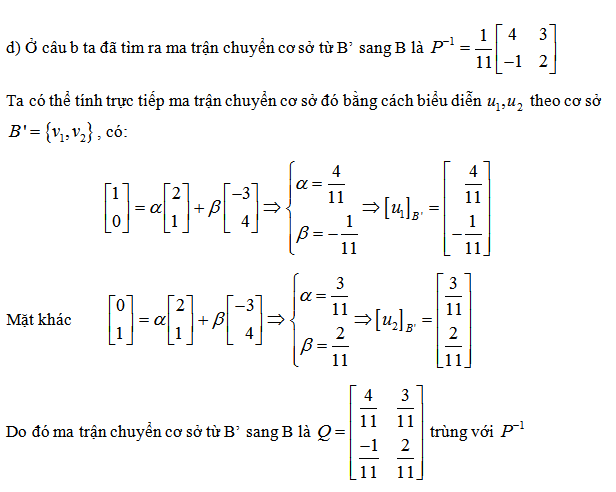

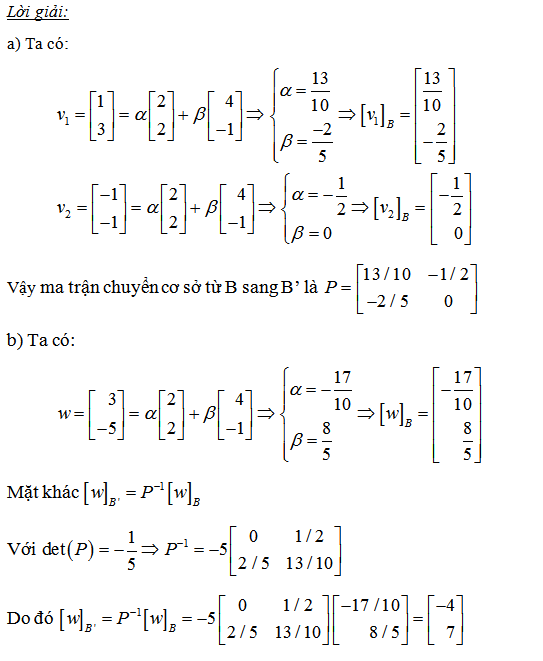

3. Tìm ma trận chuyển cơ sở


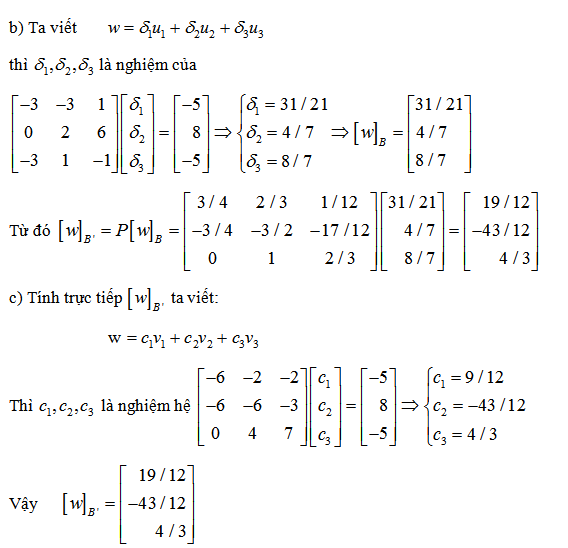


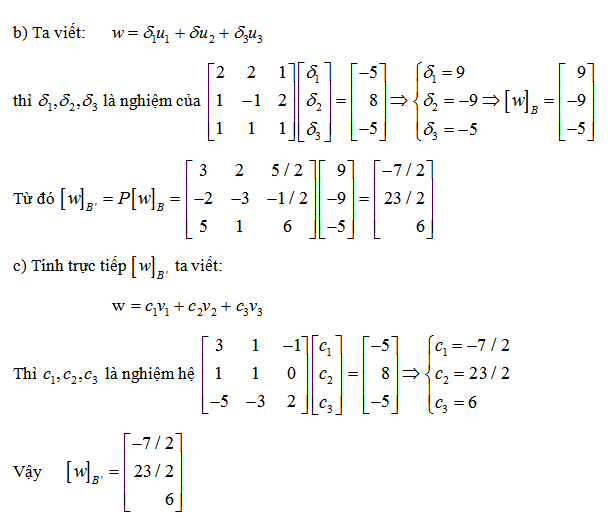
4. Tìm ma trận chuyển cơ sở kể từ u thanh lịch v


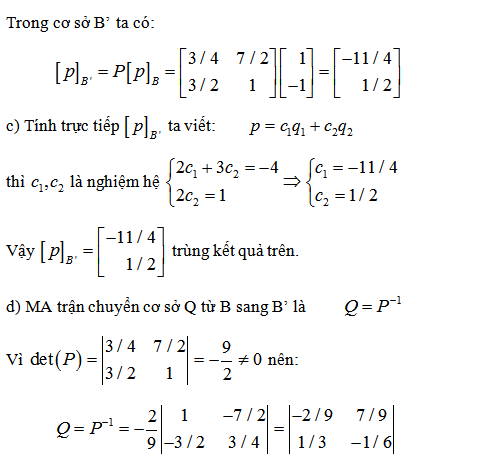

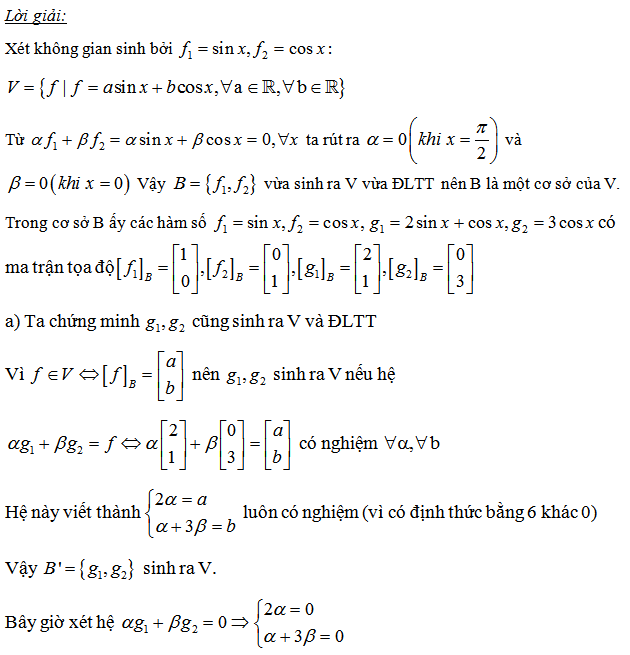
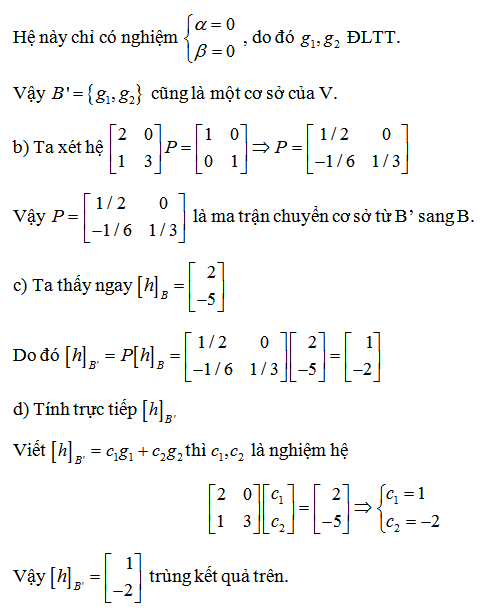
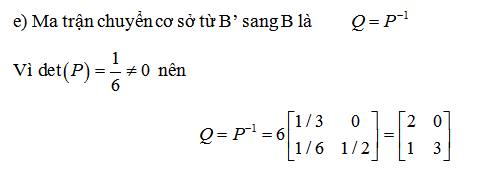
Tài liệu ma trận chuyển cơ sở PDF:
Trong nội dung bài viết này, tất cả chúng ta tiếp tục lần hiểu về định nghĩa và cách lần ma trận chuyển cơ sở. Hi vọng những bạn đã sở hữu tầm nhìn tổng quan liêu và hoàn toàn có thể triển khai những bài bác luyện tương quan. Cảm ơn chúng ta tiếp tục bám theo dõi bên trên .
Bài ghi chép liên quan:
- bài tập giải hệ phương trình vì thế cách thức cramer
- nghiệm ko tầm thường
- phép nhân 2 quái trận
- phép thế và vết của luật lệ thế
